Discrete Fourier Transform

Baron Fourier (1768-1830):
Any continuous periodic signal can be represented as the sum of carefully chosen sine waves.

The Fourier Transform is used to express a function as a continuous integral of sine waves. The Fourier Series (or Discrete Fourier Transform) is used to express a discretely sampled periodic function as a discrete sum of sine waves.

The DFT:

$F(k) & = & \sum^{N-1}_{n=0} f(n) e^{-i2\pi kn\!/N}$

and its inverse: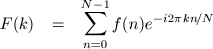

$f(n) & = & \frac{1}{N} \sum^{N-1}_{k=0} F(k) e^{i2\pi kn\!/N}$

An input series, f, of N real values fed through the forward DFT will produce an output series, F, of N/2 complex values. Obviously, the highest frequency that can be represented without aliasing given any sampling rate, R, is R/2 Hz. One-zero-one-zero at 44100Hz is a square wave with a frequency of 22050Hz. This lower frequency is called the Nyquist limit or Nyquist frequency.

The first sample of the transformed series, F₀, is the DC component (the average) of the input series.

N = number of samples R = sampling rate (samples per second) R/2 = Nyquist frequency (Hz) N/R = duration (seconds) |F[0]| = DC component Re F[n] = n-th real output Im F[n] = n-th imaginary output n*R/N = frequency (in Hz) corresponding to n-th output |F[n]| = amplitude of n*R/N Hz frequency Arg F[n] = phase of n*R/N Hz frequency

The complex output of a DFT is a polar representation of the present frequencies. The amplitude of any given frequency is the modulus of the corresponding complex output; the phase is the angle of the complex output:

$|x| & = & \sqrt{\left(\textrm{Re $x$}\right)^2 + \left(\textrm{Im $x$}\right)^2}\\ \textrm{Arg $x$} & = & \arctan \frac{\textrm{Im $x$}}{\textrm{Re $x$}}$

Example: Frequency Spectrum

nf kindly provided a 48Khz sample of him plucking the A string on his steel electric guitar. Here's a single period taken from it:

To get enough frequency resolution, I took a little more than two seconds worth of samples and ran them through a DFT (example code: dft.c - slow):

The most prominent frequency is at 107 point something Hz. The frequency of a perfectly tuned A-2 is 110Hz. The spectrum also shows diminishing overtones at integer multiples of the base frequency.